Zins- und Zinseszins
Was sind Zinseszinsen?
Als Zinseszinsen bezeichnet man Zinsen, die durch die Mitverzinsung der auf einem Konto bereits gutgeschriebenen Zinsen entstehen. Hat man 10.000 Euro auf einem Tagesgeldkonto und werden für dieses Geld in Periode 1 bei einem Zinssatz von 1,00 Prozent Zinsen in Höhe von 100 Euro gutgeschrieben, befinden sich danach 10.100 Euro auf dem Konto, die in Periode 2 weiterverzinst werden. Am Ende von Periode 2 werden dann 101 Euro an Zinsen gutgeschrieben. Die Differenz zwischen den 100 Euro Zinsgutschrift aus Periode 1 und den 101 Euro Zinsgutschrift aus Periode 2 sind die Zinseszinsen.
Der Zinseszinseffekt
Der diesem Prinzip zugrundeliegende Effekt wird als Zinseszinseffekt bezeichnet. Er bewirkt bei unveränderten Faktoren (keine Entnahme vom Konto, kein sinkender Zinssatz) ein beschleunigtes Wachstum des angelegten Kapitals, welches - das ist das grundlegende Problem des Zinseszinseffektes - bei genügend langer zeitlicher Ausdehnung gegen unendlich strebt.
Wie berechnet man Zinsen und Zinseszinsen?
Die Zinsen sind es, weswegen Anleger ihr Geld auf Tages- oder Festgeldkonten anlegen. Dabei ist eine Geldanlage umso besser, je mehr Zinsen sie erwirtschaftet. Dabei muss man zwei Elemente unterscheiden, aus denen sich die Gesamtverzinsung einer festverzinslichen Geldanlage zusammensetzt, den Zins und den Zinseszins:
- Gesamtverzinsung = Zins + Zinseszins
Der gesamte Wertzuwachs besteht also aus zwei Effekten, dem Zinseffekt und dem Zinseszinseffekt:
- Gesamter Wertzuwachs = Zinseffekt + Zinseszinseffekt
Über die Zinsen müssen wir nicht sonderlich lange reden. Ihre Berechnung ist relativ einfach und erfolgt nach folgender Formel:

Zeitraum bis zur Kapitalverdopplung
Welche Rendite bringt mir ein Zinssatz x über eine Laufzeit von y Jahren? Diese Frage wird immer wieder gestellt und lässt sich anhand unserer nachfolgenden Tabelle recht einfach beantworten:
| Zinsen in % (p.a.) |
Laufzeit in Jahren | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 10 | 20 | 30 | 40 | 50 | |||||||
| 0,010 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,10 | 0,20 | 0,30 | 0,40 | 0,50 | ||||||
| 0,020 | 0,02 | 0,04 | 0,06 | 0,08 | 0,10 | 0,20 | 0,401 | 0,602 | 0,803 | 1,005 | ||||||
| 0,030 | 0,03 | 0,06 | 0,09 | 0,12 | 0,15 | 0,30 | 0,602 | 0,904 | 1,207 | 1,511 | ||||||
| 0,040 | 0,04 | 0,08 | 0,12 | 0,16 | 0,20 | 0,401 | 0,803 | 1,207 | 1,613 | 2,02 | ||||||
| 0,050 | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,501 | 1,005 | 1,511 | 2,02 | 2,531 | ||||||
| 0,100 | 0,10 | 0,20 | 0,30 | 0,401 | 0,501 | 1,005 | 2,019 | 3,044 | 4,079 | 5,124 | ||||||
| 0,200 | 0,20 | 0,40 | 0,601 | 0,802 | 1,004 | 2,018 | 4,077 | 6,177 | 8,32 | 10,506 | ||||||
| 0,300 | 0,30 | 0,601 | 0,903 | 1,205 | 1,509 | 3,041 | 6,174 | 9,403 | 12,729 | 16,157 | ||||||
| 0,400 | 0,40 | 0,802 | 1,205 | 1,61 | 2,016 | 4,073 | 8,311 | 12,723 | 17,314 | 22,092 | ||||||
| 0,500 | 0,50 | 1,002 | 1,508 | 2,015 | 2,525 | 5,114 | 10,49 | 16,14 | 22,079 | 28,323 | ||||||
| 1,000 | 1,00 | 2,01 | 3,03 | 4,06 | 5,101 | 10,462 | 22,019 | 34,785 | 48,886 | 64,463 | ||||||
| 1,500 | 1,50 | 3,022 | 4,568 | 6,136 | 7,728 | 16,054 | 34,686 | 56,308 | 81,402 | 110,524 | ||||||
| 2,000 | 2,00 | 4,04 | 6,121 | 8,243 | 10,408 | 21,899 | 48,595 | 81,136 | 120,804 | 169,159 | ||||||
| 2,500 | 2,50 | 5,062 | 7,689 | 10,381 | 13,141 | 28,008 | 63,862 | 109,757 | 168,506 | 243,711 | ||||||
| 3,000 | 3,00 | 6,09 | 9,273 | 12,551 | 15,927 | 34,392 | 80,611 | 142,726 | 226,204 | 338,391 | ||||||
| 3,500 | 3,50 | 7,122 | 10,872 | 14,752 | 18,769 | 41,06 | 98,979 | 180,679 | 295,926 | 458,493 | ||||||
| 4,000 | 4,00 | 8,16 | 12,486 | 16,986 | 21,665 | 48,024 | 119,112 | 224,34 | 380,102 | 610,668 | ||||||
| 4,500 | 4,50 | 9,202 | 14,117 | 19,252 | 24,618 | 55,297 | 141,171 | 274,532 | 481,636 | 803,264 | ||||||
| 5,000 | 5,00 | 10,25 | 15,763 | 21,551 | 27,628 | 62,889 | 165,33 | 332,194 | 603,999 | 1046,74 | ||||||
| 5,500 | 5,50 | 11,303 | 17,424 | 23,882 | 30,696 | 70,814 | 191,776 | 398,395 | 751,331 | 1.354,196 | ||||||
| 6,000 | 6,00 | 12,36 | 19,102 | 26,248 | 33,823 | 79,085 | 220,714 | 474,349 | 928,572 | 1.742,015 | ||||||
| 6,500 | 6,50 | 13,423 | 20,795 | 28,647 | 37,009 | 87,714 | 252,365 | 561,437 | 1.141,607 | 2.230,668 | ||||||
| 7,000 | 7,00 | 14,49 | 22,504 | 31,080 | 40,255 | 96,715 | 286,968 | 661,226 | 1.397,446 | 2.845,703 | ||||||
| 7,500 | 7,50 | 15,563 | 24,23 | 33,547 | 43,563 | 106,103 | 324,785 | 775,496 | 1.704,424 | 3.618,975 | ||||||
| 8,000 | 8,00 | 16,640 | 25,971 | 36,049 | 46,933 | 115,892 | 366,096 | 906,266 | 2.072,452 | 4.590,161 | ||||||
| 8,500 | 8,50 | 17,723 | 27,729 | 38,586 | 50,366 | 126,098 | 411,205 | 1.055,825 | 2.513,302 | 5.808,632 | ||||||
| 9,000 | 9,00 | 18,81 | 29,503 | 41,158 | 53,862 | 136,736 | 460,441 | 1.226,768 | 3.040,942 | 7.335,752 | ||||||
| 9,500 | 9,50 | 19,903 | 31,293 | 43,766 | 57,424 | 147,823 | 514,161 | 1.422,031 | 3.671,94 | 9.247,726 | ||||||
| 10,000 | 10,000 | 21,000 | 33,100 | 46,410 | 61,051 | 159,374 | 572,750 | 1.644,940 | 44.25,926 | 11.639,085 | ||||||
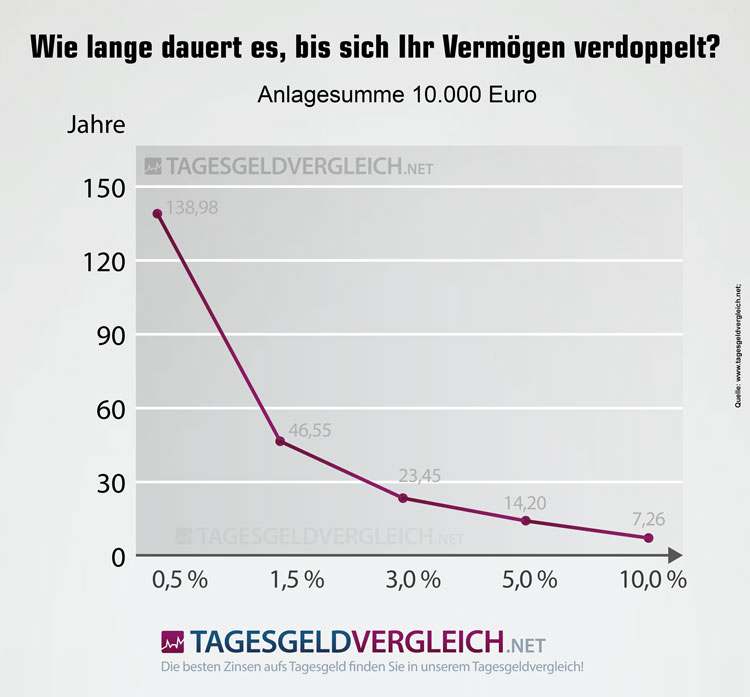
Zinsen: Wie lange dauert es, bis sich Ihr Vermögen verdoppelt?
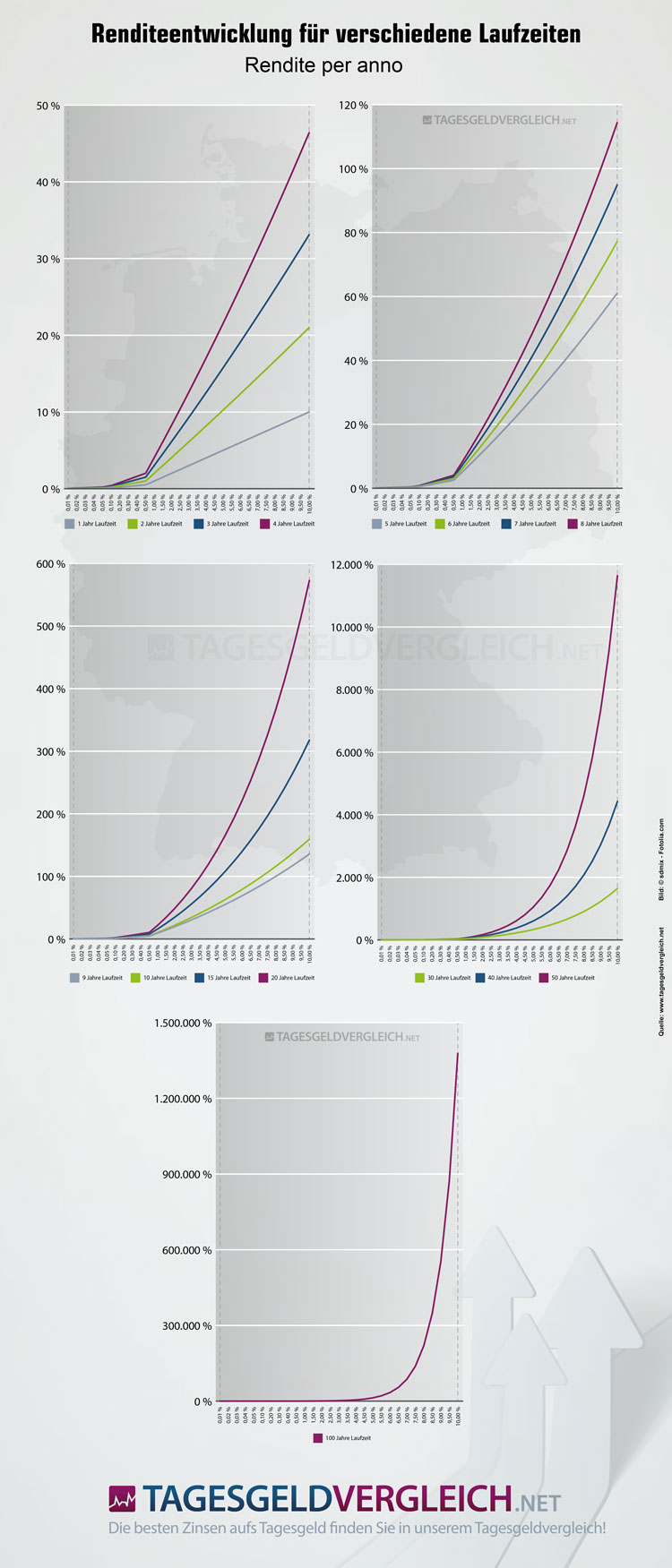
Renditeentwicklung für verschiedene Laufzeiten
Schauen wir uns das ganze an einem einfachen Beispiel an: ein Anleger hat 10.000 Euro für zehn Jahre in Festgeld angelegt, auf welches er einmal jährlich 4,50 Prozent Zinsen ausgeschüttet bekommt. Den Vermögenszuwachs innerhalb dieser zehn Jahre haben wir in folgender Tabelle aufbereitet:
| Jahr | Zu verzinsendes Kapital | Zinsen | Gesamtkapital |
|---|---|---|---|
| 1 | 10.000,- Euro | 450,- Euro | 10.450,- Euro |
| 2 | 10.000,- Euro | 450,- Euro | 10.900,- Euro |
| 3 | 10.000,- Euro | 450,- Euro | 11.350,- Euro |
| 4 | 10.000,- Euro | 450,- Euro | 11.800,- Euro |
| 5 | 10.000,- Euro | 450,- Euro | 12.250,- Euro |
| 6 | 10.000,- Euro | 450,- Euro | 12.700,- Euro |
| 7 | 10.000,- Euro | 450,- Euro | 13.150,- Euro |
| 8 | 10.000,- Euro | 450,- Euro | 13.600,- Euro |
| 9 | 10.000,- Euro | 450,- Euro | 14.050,- Euro |
| 10 | 10.000,- Euro | 450,- Euro | 14.500,- Euro |
| Gesamt | 4.500,- Euro | 14,500,- Euro |
Das Gesamtvermögen unseres Sparers ist am Ende der zehn Jahre exakt um die Summe der zehn Zinszahlungen von je 4,50 Prozent pro Jahr angewachsen.
Der Zinseszinseffekt am Beispiel - Geldanlage mit Zinseszinsen
Nun schauen wir uns das ganze für ein Tagesgeldkonto an, bei dem die ausgeschütteten Zinsen im Gegensatz zum Festgeldkonto ebenfalls mit verzinst werden. Dabei gehen wir auch hier wieder von zehn Jahren, einem Zinssatz von 4,50 Prozent pro Jahr und einer einmal jährlich erfolgenden Zinsausschüttung aus. Die Vermögensentwicklung haben wir auch für diesen Fall wieder übersichtlich aufbereitet:
| Jahr | Zu verzinsendes Kapital | Zinsen | Gesamtkapital |
|---|---|---|---|
| 1 | 10.000,00 Euro | 450,00 Euro | 10.450,00 Euro |
| 2 | 10.450,00 Euro | 470,25 Euro | 10.920,25 Euro |
| 3 | 10.920,25 Euro | 491,41 Euro | 11.411,66 Euro |
| 4 | 11.411,66 Euro | 513,52 Euro | 11.925,19 Euro |
| 5 | 11.925,19 Euro | 536,63 Euro | 12.461,82 Euro |
| 6 | 12.461,82 Euro | 560,78 Euro | 13.022,60 Euro |
| 7 | 13.022,60 Euro | 586,02 Euro | 13.608,62 Euro |
| 8 | 13.608,62 Euro | 612,39 Euro | 14.221,01 Euro |
| 9 | 14.221,01 Euro | 639,95 Euro | 14.860,95 Euro |
| 10 | 14.860,95 Euro | 668,74 Euro | 15.529,69 Euro |
| Gesamt | 5.529,69 Euro | 15.529,69 Euro |
Wie wir sehen können, bekommen wir am Ende der zehn Jahre ein etwas höheres Gesamtguthaben heraus, als beim Festgeldkonto, bei welchem die Zinsen nicht weiter verzinst wurden. Diesen Effekt nennt man Zinseszinseffekt und die zusätzlichen Zinsen bezeichnet man als Zinseszinsen. Gemäß den eingangs aufgeführten Formeln setzt sich unser Vermögenszuwachs also aus folgenden Komponenten zusammen:
- Gesamtzuwachs = 4.500,00 Euro Zinsen + 1.029,69 Euro Zinseszinsen = 5.529,69 Euro
Formeln für Zinseszins
Auch dafür gibt es Formeln, diesmal jedoch gleich zwei - eine für Sparformen mit jährlicher Zinsausschüttung und eine für Sparformen, bei denen mehrmals jährliche Zinsen ausgeschüttet werden:


Der Anfangsbetrag bezeichnet dabei das anzulegende Kapital, der Zinssatz gibt die Zinsen pro Jahr an und bei Zinszahlungen trägt man die Anzahl der Zinszahlungen pro Jahr ein. Letzteres bzw. die zweite Formel wird immer dann eingesetzt, wenn man es mit mehreren Zinsausschüttungen pro Jahr zu tun hat.
Für unser oben dargestelltes Beispiel könnten wir also anstelle der iterativen Berechnung auch die entsprechende Formel anwenden und kämen zu folgendem Ergebnis, welches mit unserer Tabelle übereinstimmt:
- 10.000 Euro x (1 + 4,5 / 100) ^ 10 = 15.529,69 Euro
Nehmen wir nun für unser oben genanntes Beispiel einmal an, die Zinsen in Höhe von 4,50 Prozent pro Jahr werden quartalsweise ausgeschüttet. Dann haben wir es mit vier Zinszahlungen pro Jahr zu tun. Für unsere angenommene Anlagedauer von zehn Jahren und das eingesetzte Kapital von 10.000 Euro würde sich nach obiger Formel folgender Endbetrag errechnen:
- 10.000 Euro x (1 + 4,50 / (100 x 4)) ^ 10 x 4 = 15.643,77 Euro
Werden die Zinsen monatlich ausgeschüttet, muss mit zwölf Zinszahlungen pro Jahr gerechnet werden, womit sich für unser oben genanntes Beispiel folgender Endbetrag errechnen lässt:
- 10.000 Euro x (1 + 4,50 / (100 x 12)) ^ 10 x 12 = 15.669,93 Euro
An diesen Beispielen kann man auch wunderbar erkennen, wie gering der Unterschied zwischen monatlicher und quartalsweiser Zinsausschüttung im Vergleich zum Unterschied zwischen jährlicher und quartalsweiser Zinsausschüttung ist. Eine entsprechende Abhandlung zu Zinsintervallen finden Sie im übrigen auf unserer folgenden Seite: Zinsintervalle beim Tagesgeld.
Mit beiden Formeln ist es auch möglich, die Gesamtverzinsung einer Geldanlage bei unterjähriger Anlagedauer zu berechnen. Hierfür muss man einfach den Prozentsatz der Jahre ansetzen, über den das Geld angelegt werden soll. Am besten lässt sich das an einem letzten Beispiel veranschaulichen: nehmen wir wieder unser oben genanntes Beispiel und monatliche Zinsausschüttung, diesmal jedoch aber nur eine Anlagedauer von neun Monaten an. Diese neun Monate entsprechen einer Anlagedauer von 9/12 Jahren oder 0,75. Setzen wir diesen Wert in die Formel ein, erhalten wir das folgende Ergebnis:
- 10.000 Euro x (1 + 4,50 / (100 x 12)) ^ 0,75 x 12 = 10.342,61 Euro
Jetzt werden Sie sich vielleicht noch fragen, wieso wir uns in allen Beispielen bezüglich der Berechnung des Zinseszinseffektes und der Zinseszinsen auf Tagesgeldkonten beruhen. Nun, das hat einen ganz einfachen Grund. Bei Festgeldkonten werden die Zinsen zwar am Ende einen jeden Jahres ausgeschüttet (bei unterjähriger Anlagedauer am Ende des vereinbarten Anlagezeitraumes), aber der angelegte Betrag wird durch sie nicht erhöht, da er fest vereinbart ist. Damit wird Jahr für Jahr nur das fest angelegte Geld verzinst, nicht aber die bereits ausgeschütteten Zinsen. Beim Tagesgeld ist das anders. Hier werden die Zinsen auf das entsprechende Tagesgeldkonto ausgeschüttet und erhöhen sofort den zu verzinsenden Betrag. Deshalb kann man beim Tagesgeld vom Zinseszinseffekt profitieren, während dies beim Festgeld nicht möglich ist!
Zins und Zinseszins berechnen
Tagesgeldzinsen berechnen
Mit unserem Tagesgeldrechner können Sie Zins und Zinseszinsberechnungen für beliebige Anlagesummen, Zinsintervalle und auch für verschiedene Methoden der bankseitigen Zinsberechnung durchführen:
Tages- und Festgeldzinsen vergleichen
Mehr als 100 Tages- und 70 Festgeldkonten, mit denen Sie den Zinseszinseffekt ausnutzen können, finden Sie in unseren Vergleichen: